datStruct-4

BINARY SEARCH TREE

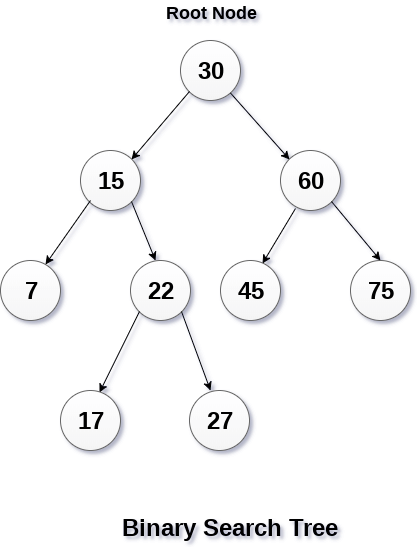
Binary search tree(BST) adalah bentuk turunan dari binary tree. binary tree adalah tree yang hanya memiliki 2 node. pada BST, node kiri selalu bernilai lebih rendah dan node kanan selalu bernilai lebih besar.

*Dengan BST, segala insertion, deletion, dan search dapat dilakukan dalam Olog(N) (N=jumlah node pada tree). Akan berguna dalam kasus N nya berjumlah banyak.

*Karena semua tersusun dengan rapi, maka pencarian dapat dilakukan dengan mudah.

3 Operation utama dalam BST:
1. find()
2. insert()
3. remove()








INSERT()

insert(x,root)// node dimulai dari root karena root merupakan level paling dasar pada tree.

(t == null) // artinya node tersebut belum terpakai dan node baru akan disimpan di tempat itu sebagai leaf (left dan right = NULL)



//bila x lebih kecil dari node, maka lakukan insert dengan node->left sebagai node currentnya. begitu juga bila x lebih besar, maka node->right sebagai node current.






REMOVE()

untuk remove(), perlu diperhatikan apabila node yang dihapus bukan leaf (node memiliki 2 sub tree), maka node itu perlu di replace dengan kanan paling kecil atau kiri paling besar









//findMin(t->right) : untuk mencari node terkecil pada right sub tree
//node yang akan di remove di replace dengan temp
//kemudian lakukan remove pada node original yang digunakan pada temp
//deletion bisa juga menggunakan findMax(t->left) ,dengan kiri paling besar


//bila node yang ingin dihapus hanya memiliki 1 child, maka hubungkan parent dari node dengan child dari node










FIND()

//jika key lebih besar daripada current node, maka node yang dicari pasti berada di kanan current node
jika lebih kecil, maka di kiri.