DatStruct-10

AVL

Pada Binary Tree, ada sebuah kekurangan pada bagian insert yaitu jika kita insert dengan value 1-10 secara berurutan, maka untuk mencari nilai 10 perlu traverse dari 1-10, dengan kata lain 10x pencarian.

Untuk membuat pencarian dalam binary tree menjadi sebuah struktur data yang lebih efektif, kita menggunakan AVL tree, yaitu sebuah teknik develop yang di oleh Adelson, Velskii, dan Landi , dimana ketinggian dari left dan right subtree tidak lebih dari 1 node.

Intinya, setiap kali melakukan insertion, program ada mengecek apakah tree seimbang atau tidak.

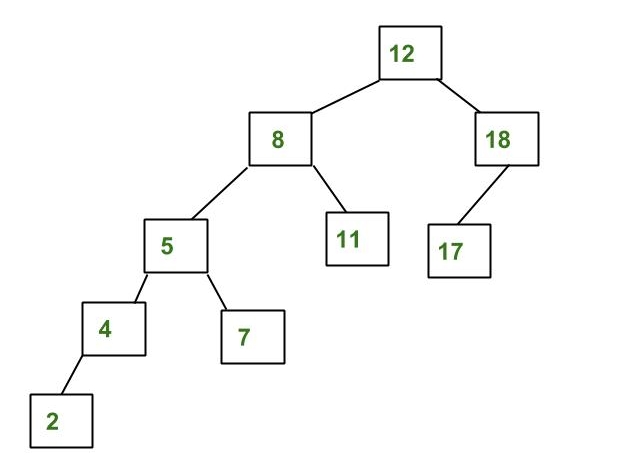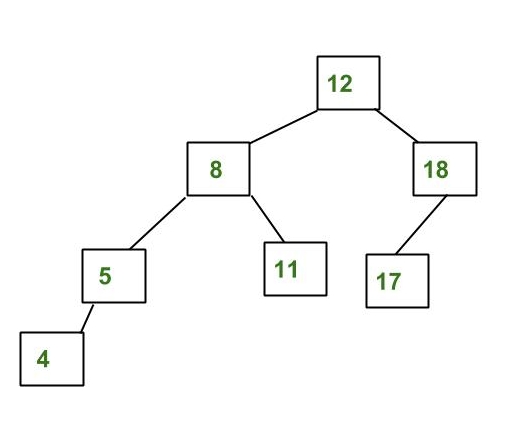
Not Balanced

Balanced

Pada AVL Tree, kita menambahkan suatu attribut pada setiap node yang bernama 'BALANCE FACTOR", fungsinya sebagai indikator apakah node tersebut seimbang atau tidak.

Pada gambar di atas (Balanced),  Node 12 memiliki balance factor bernilai -1, karena,

Right's height: 2 | left's height: 3 

Right - Left = -1,

artinya, Balance Factor pada node 12 termasuk seimbang karena tidak lebih dari 1 atau kurang dari -1.

Pada gambar di atas (Not Balanced), Tree tersebut tidak seimbang karena Node 8 memiliki Balance Factor -2. Untuk menyeimbangkan Tree, AVL menggunakan teknik yang dinamakan "ROTATE".

Rotate dibagi menjadi 4 kasus (Berdasarkan posisi node paling bawah):

1. Left Left

*pada contoh di bawah, 8 dan 12 memiliki balance factor -2, namun yang di rotate adalah Node 8 terlebih dahulu, jadi yang di bawah diutamakan.

              12                                                                        12
             /    \                                                                      /    \
          8        18          ---------------------->                        5      18
         /  \         /            Right Rotate (8)                         /  \       /
       5    11    17                                                            4   8    17
      /                                                                             /       \
    4                                                                            2         11
    /                               
 2

2. Left Right

*tidak seimbang pada node 15 (-2), pada kasus ini lakukan:
  1. Left rotate pada left child of 15, yaitu 8
  2. Right rotate pada 15

                                                   (Hasilnya menjadi spt kasus 1)
              15                                                      15                                                      10               
             /    \                                                    /    \                                                  /       \             
          8        18         ----------------->           10     18     ------------->                      8         15           
         /  \                    Left Rotate (8)           /    \           Right Rotate(15)            /  \        /   \         
       7    10                                                 8     12                                             7     9   12    18   
             /   \                                               /  \                                                                               
           9     12                                          7    9                                                                                  
                                 

3. Right Right

                 15                                                                            17                               
                /    \                                                                       /         \                               
              8       17               ----------------->                         15        19                                                 
                      /    \             Left Rotate(15)                        /    \       /   \                                         
                    16    19                                                        8    16   18   20                             
                           /    \                                                                                         
                         18    20                                                                                                 
                                                                                                                         
4. Right Left
                                                                                       
           15                                                      15                                                         17
          /    \                                                   /     \                                                      /     \
        8      20           -------------------->        8      17        ----------------->                 15     20               
                /   \           Right Rotate (20)              /  \       Left Rotate (15)              /    \        \         
              17   22                                              16   20                                         8      16     22
             /                                                                   \       
          16                                                                    22       

*Ada kemungkinan meski sudah melakukan rotate, namun tetap tidak seimbang, maka lebih mudah jika menggunakan fungsi rekursif.